Diffraction
There are phenomena in some areas of physics that cannot be explained in a geometrical sense. A simple example: a water wave reaches a harbour entrance. If this entrance is very narrow a wave develops that looks as if a stone was thrown in the harbour entrance. Depending on where you’re standing you can see the wave but you can’t necessarily see the boat that caused the wave.
The same applies to light: picture light as a particle. If a camera shoots this particle in the direction of the aperture then the light should spread straight-lined and hit the sensor behind the aperture. But that is not the case. Light falls into areas you wouldn’t expect it to be if it was a particle that flies through the lens.
So even with the best lens a so-called Airy circle occurs that becomes wider the smaller the aperture gets.
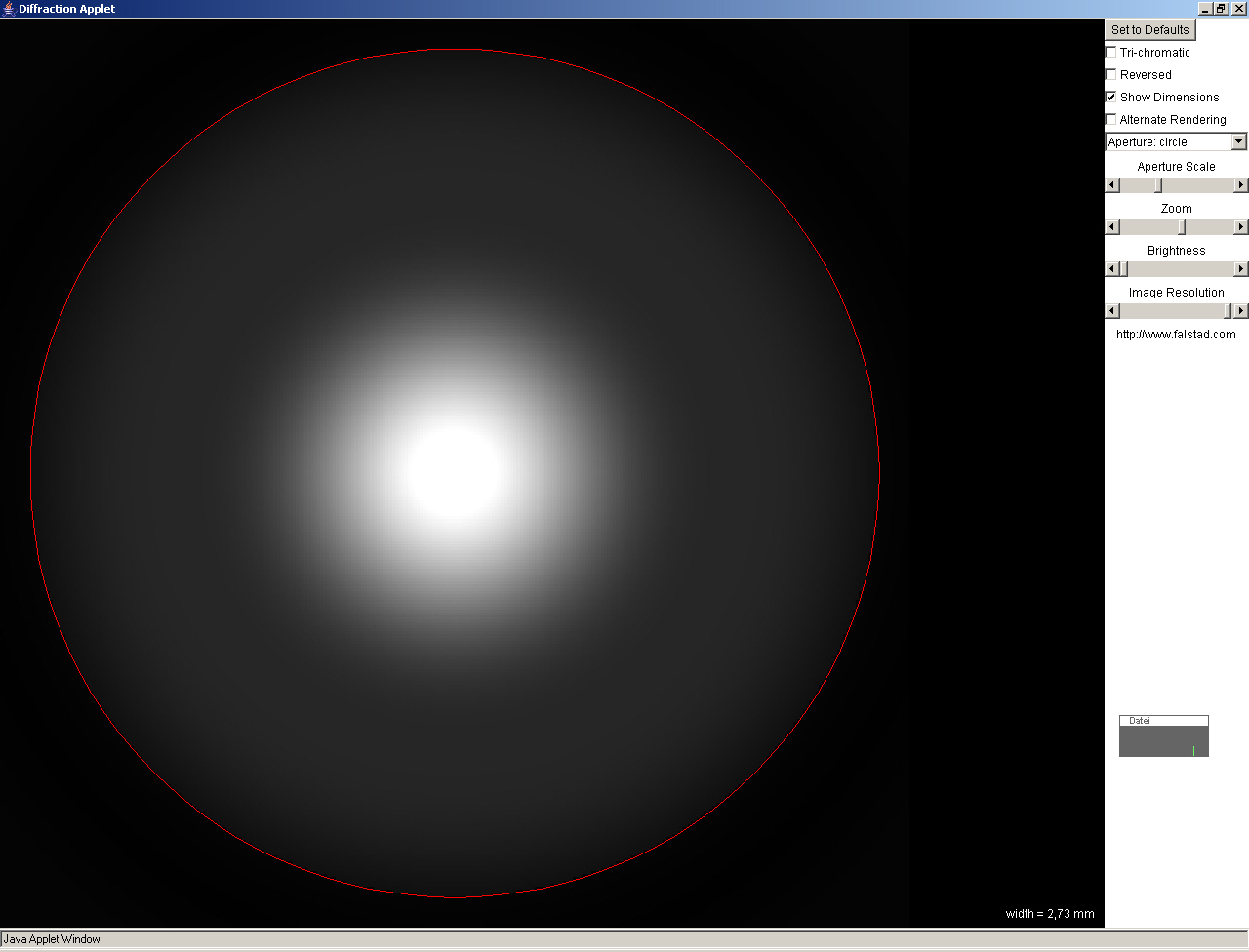
The diffraction image shows a bright center that is surrounded by bright and dark rings. The brightness decreases fast to the outside.
The radius of the Airy circle / the bright center is calculated like this:
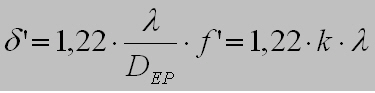
with
d’ = radius of the Airy-circle
lambda = lenght of lightwaves
DEP = diameter of entrance pupil
K = f-stop
The higher the f-stop setting is the bigger the Airy circle. The question now is: “At which point does the diffraction become a limiting factor for detail reproduction, hence the resolution?”
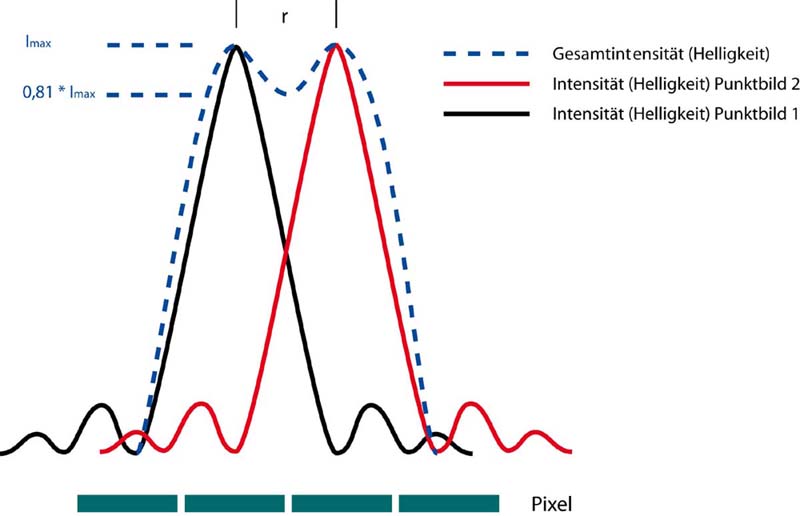
In order to answer this, the first thing is to test when a person sees Airy circles as separate points. Lord Raleigh implemented and published this test in 1879. It shows that the intensity of the area which is in between two of those slices must have downgraded to 81 % of the maximum magnitude in order for the eye to recognize separate slices. This happens when the maxima of the Airy circles have the distance of a circle’s radius.
The radius of an Airy circle that gets transferred to the pixels of a digital camera should be smaller than the distance between 2 pixels. We have to know the size of a pixel in order to define the size of the acceptable Airy circle and with that the smallest aperture where the diffraction doesn’t limit resolution. To do this we can divide the width of the sensor with the number of pixels and we have the size of one pixel.
This shows the diffraction figure of two dots. If they have a gap that matches with the gap of the radius, they are just visible with a sufficient zoom.
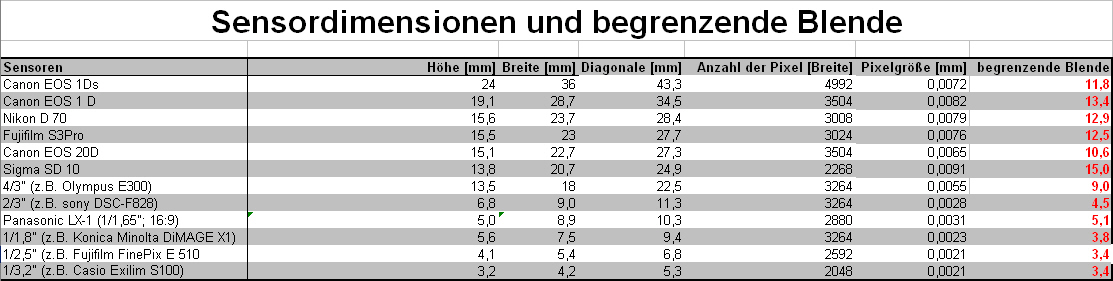
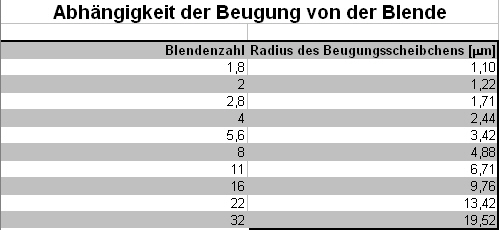
The table indicates the limiting apertures (right column) for the listed cameras. With smaller apertures (higher f-stops) diffraction limits the resolution ability of the camera.
As the table with the limiting aperture shows, the resolution limit for digital SLR- cameras through diffraction usually starts with aperture 11. A loss of resolution is already visible starting from f-stop 4 in consumer cameras.
Our demonstration pictures from Panasonic LX-1 show a worsening of resolution happens at f-stop 5.6.
Every picture shows the center of one of our demonstration pictures, taken with Panasonic LX-1, f-stop 4, 5.6 and 8 (left to right). It is recognizable that the resolution deteriorates through diffraction with f-stop 5.6.
Conclusion
When considering diffraction, digital cameras with bigger pixels have advantages because smaller apertures up to f-stop 11 can be used without worsening the resolution. Big pixels are usually found in ’single lens reflection’ systems with big sensors. Be careful not to stop down too much with consumer cameras that have smaller pixels, otherwise the resolution quality will obviously suffer. When considering depth of field, the diffraction takes a subordinated role because the limiting aperture is bigger with a smaller sensor but on the other hand the depth of field increases.